Linhas de Transmissão

Circuito Equivalente de uma Linha de Transmissão

Detalhes

Criado em Quarta, 31 Agosto 2011 01:16

Última atualização em Sábado, 09 Junho 2012 15:08

Escrito por Eduardo Faustino Coelho

Acessos: 3496

Como vimos no post anterior “Características das Linhas de Transmissão”, a principal diferença entre uma linha de transmissão (ou qualquer sistema de guiagem de ondas) e um condutor é a “dependência de posição”: ao longo de um trecho de linha de transmissão, as tensões e correntes, não dependem apenas do tempo, mas também da distância à fonte ou à carga. Uma vez que tensões e correntes não são constantes ao longo da linha, a impedância também não é constante. Para entender melhor a dependência de posição, devemos determinar e equação da LT.

Porém, antes de determinar a equação da LT precisamos conhecer o circuito equivalente das LT’s. O circuito equivalente é estabelecido com base no efeito da geometria da LT sobre os campos elétrico e magnético presentes na linha.

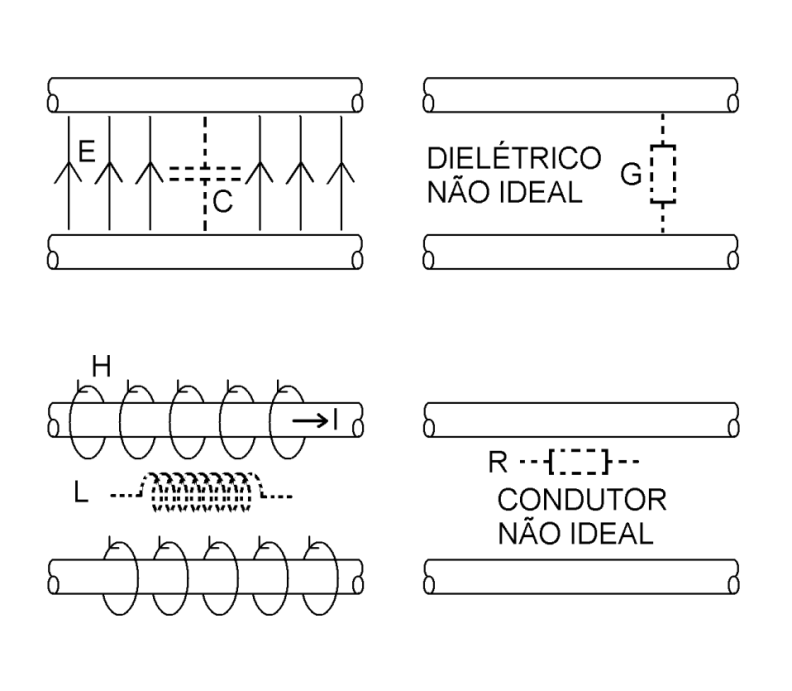
A diferença de potencial entre os condutores da linha de transmissão estabelece um campo elétrico entre esses eles. Sempre que temos duas superfícies condutoras isoladas uma da outra com um campo elétrico entre elas, cargas acumulam-se nessas superfícies condutoras, e o conjunto de condutores, cargas e campo elétrico definem um capacitor. Em outras palavras, a geometria da LT determina a existência de um capacitor em paralelo com os condutores. O valor da capacitância depende da geometria e materiais da LT, mas é sempre proporcional ao comprimento da LT.

A corrente que flui pelos condutores da linha de transmissão estabelece um campo magnético ao redor deles. Sempre que temos condutores próximos a um campo magnético, correntes serão induzidas nesses condutores (indutância própria e mútua) e o conjunto de condutores correntes e campo magnético definem um indutor. Em outras palavras, a geometria da LT determina a existência de um indutor em série com os condutores. O valor da indutância depende da geometria e materiais da LT, mas é sempre proporcional ao comprimento da LT.

Em uma linha de transmissão real, os condutores apresentam alguma resistividade que vai dissipar uma parte de energia que se propaga por ela. Em outras palavras, o circuito equivalente de um LT real precisa incluir um resistor em série com os condutores que representa as perdas devidas à dissipação de energia nestes. O valor desse resistor depende da geometria e materiais da LT, mas é sempre proporcional ao comprimento da LT.

Em uma linha de transmissão real, dielétrico que separa os condutores apresenta alguma condutividade que vai dissipar uma parte de energia que se propaga por ela. Em outras palavras, o circuito equivalente de um LT real precisa incluir uma condutância em paralelo com os condutores que representa as perdas devidas à dissipação de energia no dielétrico. O valor dessa condutância depende da geometria e materiais da LT, mas é sempre proporcional ao comprimento da LT.

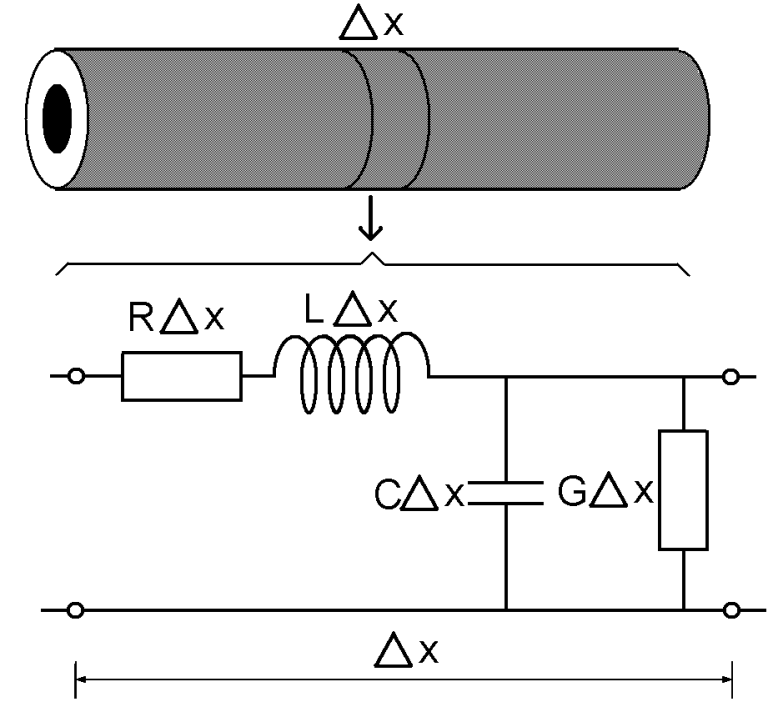
Todos os quatro componentes do circuito equivalente da LT têm seus valores proporcionais ao comprimento do trecho de LT a ser analisado. Para estabelecer a equação de onda da LT vamos começar com um trecho de LT de comprimento Δx e depois determinar o limite quando Δx tende a zero.

O circuito equivalente de um trecho de LT de comprimentoΔ x é representado abaixo. A capacitância distribuída por unidade de comprimento devida ao campo elétrico entre os condutores é de C(F/m), logo num trecho de comprimentoΔ x a capacitância é CΔ x (F). Da mesma forma, a indutância distribuída por unidade de comprimento é L(H/m) e, num trecho de comprimentoΔx, a indutância é LΔ x (H). A resistência distribuída por unidade de comprimento devida às perdas no condutor é R(Ω/m) e, num trecho de comprimento Δx, a resistência é RΔx (Ω). A condutância distribuída por unidade de comprimento devida às perdas no dielétrico é G (S/m) e, num trecho de comprimentoΔx, a condutância é GΔx (S).

Para determinar a equação da LT, vamos aplicar as Leis de Kirchoff ao circuito equivalente de um trecho de LT de comprimento Δ x. A aplicação da LKT resulta na equação:

$$V(x)=(R+j\Omega L)\Delta xI(x)+V(x+\Delta x$$

Por outro lado, a aplicação da LKC resulta:

$$I(x)=(G+j\omega C)\Delta x V(x+ \Delta x)+I(x + \Delta x)$$

Dividindo por Δx, fazendo Δx tender a zero e eliminando os termos em Δx2 resulta:

$$\Delta x \rightarrow \partial x$$

$$\frac{\partial V(x)}{\partial x}=-(R+j \omega L)I(x)$$

$$\frac{\partial I(x)}{\partial x}=-(G+j \omega C)V(x)$$

Onde ??é a frequência angular dada por ????f. Derivando a aplicação da LKT em relação a x uma segunda vez e substituindo a expressão da derivada parcial de I(x) em x escrita acima, resulta:

$$\frac{\partial^2 V(x)}{\partial x^2}-(R+j \omega L)(G+j \omega C)V(x)=0$$

Analogamente,

$$\frac{\partial^2 I(x)}{\partial x^2}-(R+j \omega L)(G+j \omega C)I(x)=0$$

Essas são as equações diferenciais das linhas de transmissão (Equações dos Telegrafistas) cujas soluções são:

$$V(x)=V^+ e^{- \gamma x}+V^-e^{+ \gamma x}$$

$$I(x)=I^+ e^{- \gamma x}-I^- e^{+ \gamma x}$$

Onde,

$$\gamma = \sqrt{(R+j \omega L)(G+j \omega C)}$$