Linhas de Transmissão

Solução da Equação da LT

Detalhes

Criado em Segunda, 12 Setembro 2011 00:34

Última atualização em Domingo, 10 Junho 2012 20:40

Escrito por Eduardo Faustino Coelho

Acessos: 2625

No artigo anterior deduzimos a equação diferencial das linhas de transmissão ou "Equação dos Telegrafistas" como é chamada nos livros mais antigos. Nesse artigo vamos examinar a solução da Equação da LT para compreender os conceitos de onda direta e refletida, impedância característica e impedância localizada.

Como vimos no artigo anterior “Circuito Equivalente de uma Linha de Transmissão”, a solução do circuito equivalente da LT são duas equações diferenciais chamadas de Equações dos Telegrafistas da forma:

$$\frac{\partial^2 V(x)}{\partial x^2}-(R+j \omega L)(G+j \omega C)V(x)=0$$

e

$$\frac{\partial^2 I(x)}{\partial x^2}-(R+j \omega L)(G+j \omega C)I(x)=0$$

e que têm como soluções as expressões:

$$V(x)=V^+ e^{- \gamma x}+V^-e^{+ \gamma x}$$

$$I(x)=I^+ e^{- \gamma x}-I^- e^{+ \gamma x}$$

$$\gamma = \sqrt{(R+j\omega L)(G+j\omega C)} $$

No artigo anterior fizemos referência a ? ser a frequência angular dada por ????f . Em outras palavras, estamos usando o regime senoidal permanente, que será melhor explicado em um artigo de eletricidade básica. No momento, o importante é saber que V(x) e I(x) são fasores, e que um fasor, é uma forma de representar uma tensão ou corrente que estão em regime senoidal permanente. Por exemplo, uma tensão v(t) é representada no regime senoidal permanente pelo fasor V e que a relação entre v(t) e o fasor V é:

$$ v(t)=Re{Ve^{j\omega t}}= V sen( \omega t)$$

ou seja, as expressões das tensões e correntes correspondentes às soluções da equação da LT, são dadas por:

$$ v(x,t)=Re \left \{(V^+ e^{- \gamma x}+V^- e^{+ \gamma x}) e^{j \omega t} \right \} $$

$$v(x,t)=(V^+ e^{- \alpha x} cos( \omega t- \beta x)+V^- e^{+ \alpha x}) cos( \omega t + \beta x) $$

$$i(x,t)=Re \left \{(I^+ e^{- \gamma x}-I^- e^{+ \gamma x}) e^{j \omega t} \right \} $$

$$i(x,t)=(I^+ e^{- \alpha x} cos( \omega t- \beta x)-I^- e^{+ \alpha x}) cos( \omega t + \beta x)$$

os termos V+ e V- correspondem às ondas que se propagam no sentido da fonte para a carga (incidente) e da carga para a fonte (refletida). No início causa estranheza o termo  estar associado a –jβ e vice-versa, mas o motivo pode ser perfeitamente entendido se fixarmos atenção nos termos:

$$ \phi _1 = \omega t - \beta x $$

$$ \phi _2 = \omega t + \beta x$$

Os termos acima são chamados “fases” da onda transmitida e refletida, respectivamente. Para entender o significado físico da fase, devemos ter em mente o movimento das ondas do mar. Veja a figura abaixo:

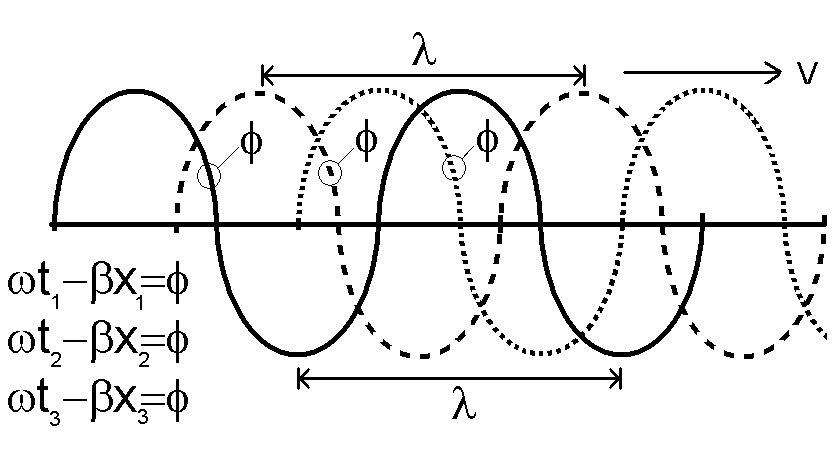
Cada “região” da onda (flanco de subida ou descida, pico ou ventre) que vemos mover-se está associada a um certo valor de fase. Por exemplo, no caso de uma onda associada a uma função seno, o pico e o ventre estão associados a valores de fase próximos de 90 e 270 graus, respectivamente, os flancos de subida e descida a valores de 0 e 180 graus, respectivamente.

Agora, vamos fixar a atenção apenas na fase da onda transmitida:

$$ \phi _1 = \omega t - \beta x $$

Note que à medida que o tempo cresce, o produto da frequência angular pelo tempo também precisa aumentar. Note também que, para a onda “andar para frente”, a distância x precisa crescer à medida que o tempo cresce (se a distância reduzisse, a onda estaria andando para trás). Se o coeficiente que multiplica x fosse positivo, quando t e x crescessem ao mesmo tempo, a soma dos termos em x e t cresceria também, logo a fase não poderia ficar constante. Por outro lado, se os termos em x e t têm sinais oartigoos, x e t podem aumentar ao mesmo tempo e a fase poderá ficar constante, desde que a razão do crescimento da distância x em relação ao tempo t tenha um valor adequado. Vamos determinar essa razão de crescimento.

Para isso, vamos supor que em certo instante de tempo t0, estamos observando um ponto que tenha certo valor de fase:

$$ \phi _0 = \omega t_0 - \beta x_0 $$

Após um intervalo de tempo, continuamos a observar o mesmo ponto da onda. Assim, mesmo que os fatores e x e t tenham mudado de valor, a soma dos dois permanece constante:

$$ \phi _0 = \omega t_0 - \beta x_0 + \omega \Delta t - \beta \Delta x $$

para que isso aconteça é necessário que:

$$ \omega \Delta t - \beta \Delta x = 0$$

ou seja, a taxa de variação da distância com o tempo seja:

$$ v_f = \frac{\Delta x}{\Delta t}= \frac {\omega}{\beta} $$

note que “taxa de variação da distância com o tempo” é aquilo que chamamos de velocidade. Essa velocidade dos pontos de fase constante é chamada “velocidade de fase”.

Como já escrevemos em artigos anteriores, tensões e correntes não são uniformes ao longo de uma linha de transmissão. Consequentemente, a impedância que é a razão entre a tensão e a corrente também não será constante, ou em outras palavras, também manifestará dependência de posição.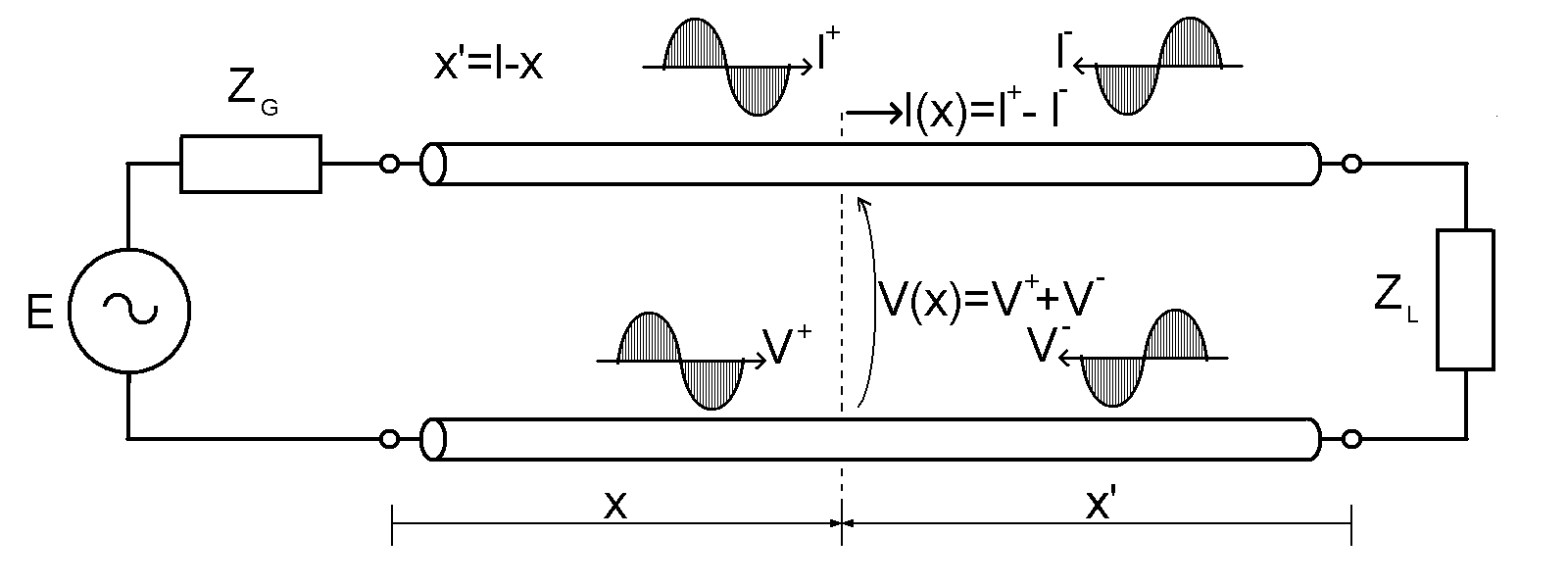



Para entender como a impedância varia ao longo de uma linha de transmissão, vamos começar com uma expressão que vimos no artigo sobre a equação da LT.

$$\frac{\partial V(x)}{\partial x}=-(R+j \omega L)I(x)$$

Por outro lado, ao resolvermos a equação da LT, encontramos a seguinte expressão para a tensão ao longo da LT:

$$V(x)=V^+ e^{- \gamma x}+V^-e^{+ \gamma x}$$

Se aplicarmos a definição de derivada em relação a x à expressão acima teremos:
$$\frac{\partial V(x)}{\partial x}=\gamma (V^+ e^{- \gamma x}+V^-e^{+ \gamma x})$$
ou ainda,
$$-(R+j \omega L) (I^+ e^{- \gamma x}-I^-e^{+ \gamma x})=\gamma (V^+ e^{- \gamma x}+V^-e^{+ \gamma x})$$
Nesse caso, então:
$$\frac{V^+}{I^+}=\frac{V^-}{I^-}=Z_0=\frac{\gamma }{(R+j \omega L)}= \sqrt{\frac{(R+j\omega L)}{(G+j\omega C)}}  $$
A relação entre tensões e correntes que se propagam no mesmo sentido é chamada impedância característica, é uma propriedade intrínseca da LT, mas ainda não é a relação entre a tensão e a corrente que se observa a uma distância x do gerador. Essa relação é chamada impedância localizada e é dada pela expressão:
$$Z(x)=\frac{V(x)}{I(x)}=\frac{V^+ e^{- \gamma x}+V^-e^{+ \gamma x}}{\frac{V^+}{Z_0} e^{- \gamma x}-\frac{V^-}{Z_0}e^{+ \gamma x}} $$
Que pode ser ainda reescrita como:
$$Z(x)=Z_0 \frac{1+( \frac{V^-}{V^+} ) e^{2 \gamma x}}{1-\frac{V^-}{V^+} e^{2 \gamma x}} $$
Essa expressão será útil para compreendermos o conceito de coeficiente de reflexão, que é fundamental para examinarmos as ondas estacionárias, mas esses serão assuntos de artigos futuros, até a próxima...