A primeira reação de qualquer aluno de eletromagnetismo ou telecomunicações ao se deparar com a CS é de aversão, afinal aquele monte de círculos espalhados de forma estranha uns por dentro dos outros parece tudo menos eletrônica. Ao pesquisar a CS na internet com o Google, uma das primeiras imagens que aparece tem o subtítulo de “Black Magic Design”, mas uma, vez compreendida, a CS se torna um poderoso auxiliar para simplificar o trabalho tedioso de cálculo envolvido em circuitos de RF e permitir uma visualização dos fenômenos que ocorrem dentro de uma estrutura de guiagem de ondas eletromagnéticas.
Para entender o funcionamento da CS, vamos voltar às expressões do coeficiente de reflexão e da impedância localizada ao longo da LT:
$$ \Gamma_L = \frac{Z_L-Z_0}{Z_L+Z_0} $$
$$ Z(d)=Z_0 \frac{1+\Gamma_L e^{- j2 \beta d}}{ 1- \Gamma_L e^{-j2 \beta d} }$$
A expressão do coeficiente de reflexão pode ser reescrita da seguinte forma:
$$Z_L = Z_0 \frac {1+ \Gamma_L}{1-\Gamma_L} = Z_0 \frac {1+\Gamma_L e^j0}{1-\Gamma_L e^j0}$$
Ou seja, a impedância da carga, é dada pela expressão da impedância localizada para d=0. Além disso, devemos ter em mente que o coeficiente de reflexão da carga é uma grandeza complexa que pode ser representada na forma de parte real e imaginária, mas também na forma de módulo e fase:
$$ \Gamma_L = \left| \Gamma_L \right| e^{j\phi_L}$$
Assim, a impedância localizada ao longo da linha pode ser escrita pela fórmula:
$$ Z(d)=Z_0 \frac{1+\left | \Gamma_L \right | e^{j(\phi_L- j2 \beta d)}}{ 1- \left | \Gamma_L \right | e^{j(\phi_L-j2 \beta d)} }$$
E podemos definir o coeficiente de reflexão localizado dado por:
$$ \Gamma(d)= \left | \Gamma_L \right | e^{j(\phi_L- j2 \beta d)}$$
Assim,
$$ Z(d)=Z_0 \frac{1+\Gamma (d) } { 1 - \Gamma (d) }$$
Agora que apresentamos o coeficiente de reflexão localizado, vamos à CS. A CS é um gráfico com um sistema de coordenadas bem particular.
Nos artigos sobre ondas estacionárias, a impedância localizada da LT era sempre mostrada em gráficos de Re[Z(d)] ou Im[Z(d)] em função da distância à carga d, ou seja, o sistemas de coordenadas é formado pela distância à carga (abcissas) e pela parte real ou imaginária da impedância localizada (ordenadas). A CS também é um gráfico, mas suas coordenadas são x e h dados por:
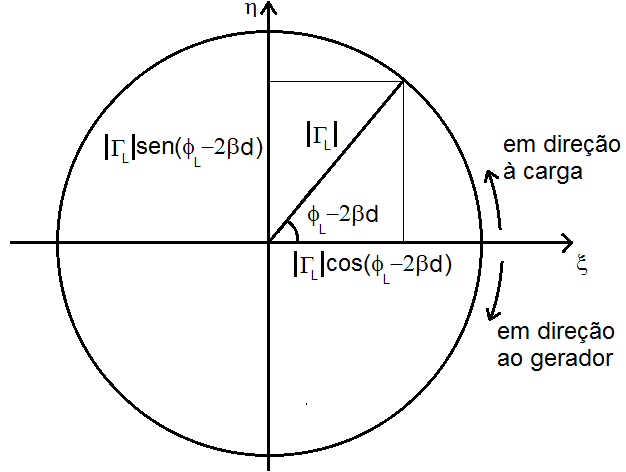
$$ \xi = \left | \Gamma_L \right | cos(\phi_L – 2 \beta x) $$
$$ \eta = \left | \Gamma_L \right | sen(\phi_L – 2 \beta x) $$
$$ \Gamma(d)= \left | \Gamma_L \right | e^{j(\phi_L- j2 \beta d)}=\left | \Gamma_L \right | cos(\phi_L – 2 \beta x)+j\left | \Gamma_L \right | sen(\phi_L – 2 \beta x)$$
Vai sempre se localizar em um círculo de centro na origem e raio igual ao módulo de GL. Quando nos deslocamos sobre a LT em direção ao gerador, a distância à carga d aumenta e o argumento fL – 2bd diminui, ou seja quando nos afastamos da carga (direção do gerador), percorremos o círculo no sentido horário. Analogamente, quando nos deslocamos na LT em direção à carga, a distância à carga d diminui e o argumento fL – 2bd aumenta, assim, quando nos aproximamos da carga (direção da carga), percorremos o círculo no sentido anti-horário. Veja a figura:
E como ficam os valores de impedância localizada no “plano do coeficiente de reflexão”? A impedância localizada, como já vimos, é expressa em função do coeficiente de reflexão localizado por:
$$ Z(d)= R(d) +jX(d) =Z_0 \frac{1+\Gamma (d) } { 1 - \Gamma (d) }$$
Existem muitos livros sobre circuitos de RF que apresentam a dedução dos círculos de resistência e reatância constante a partir da expressão de Z(d), x e h, isso não será feito aqui, uma vez que os detalhes matemáticos da construção da CS não auxiliam a entender seu uso. O importante é saber que:
- Na CS os valores de resistência e reatância estão “normalizados”, ou seja, divididos pela impedância característica da LT Z0.
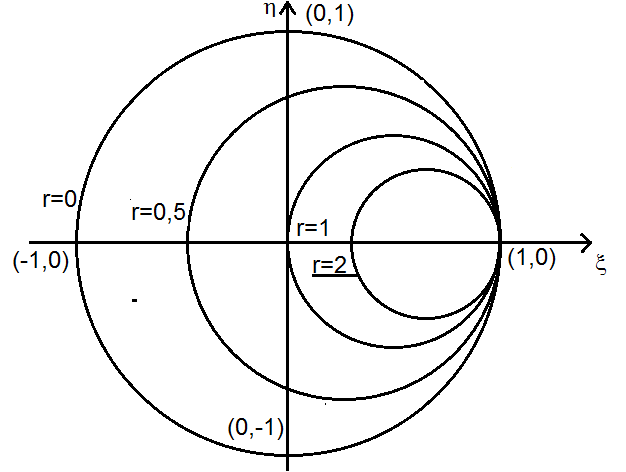
- O “lugar geométrico” dos pontos de resistência constante e igual a r, é um círculo de centro:
$$ (\frac{r} {r+1}, 0) $$
e raio igual a
$$ \frac{1}{r+1} $$
Veja a figura:
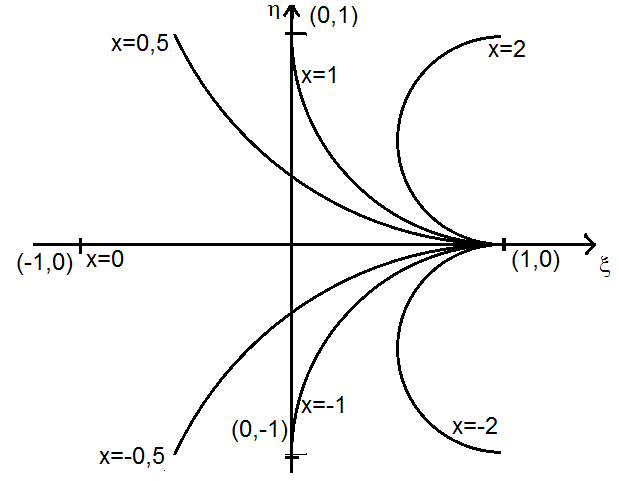
O “lugar geométrico” dos pontos de reatância constante e igual a x, é um círculo de centro:
$$ (1, \frac{1} {x}) $$
e raio igual a
$$ \frac{1}{x} $$
Veja a Figura:
Quando os círculos de resistência e reatância constante são plotados em conjunto surge o aspecto característico da Carta de Smith. Veja a Figura:
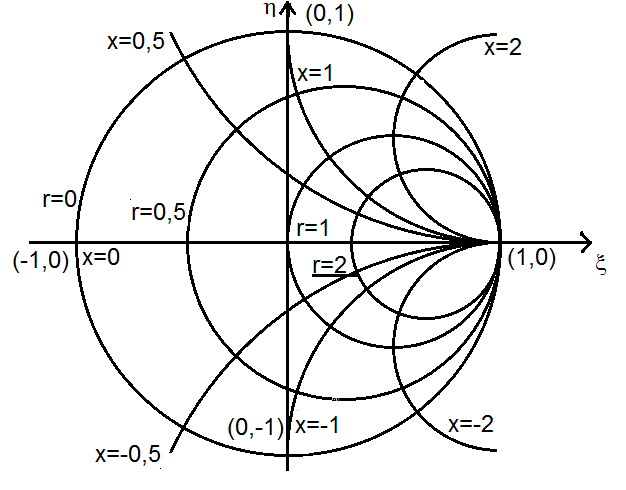
Nos artigos seguintes vamos mostrar como a Carta de Smith simplifica o trabalho tedioso de cálculo de circuitos de RF.
Veja Também:
Baixe a carta de Smith clicando aqui